RSA加密算法
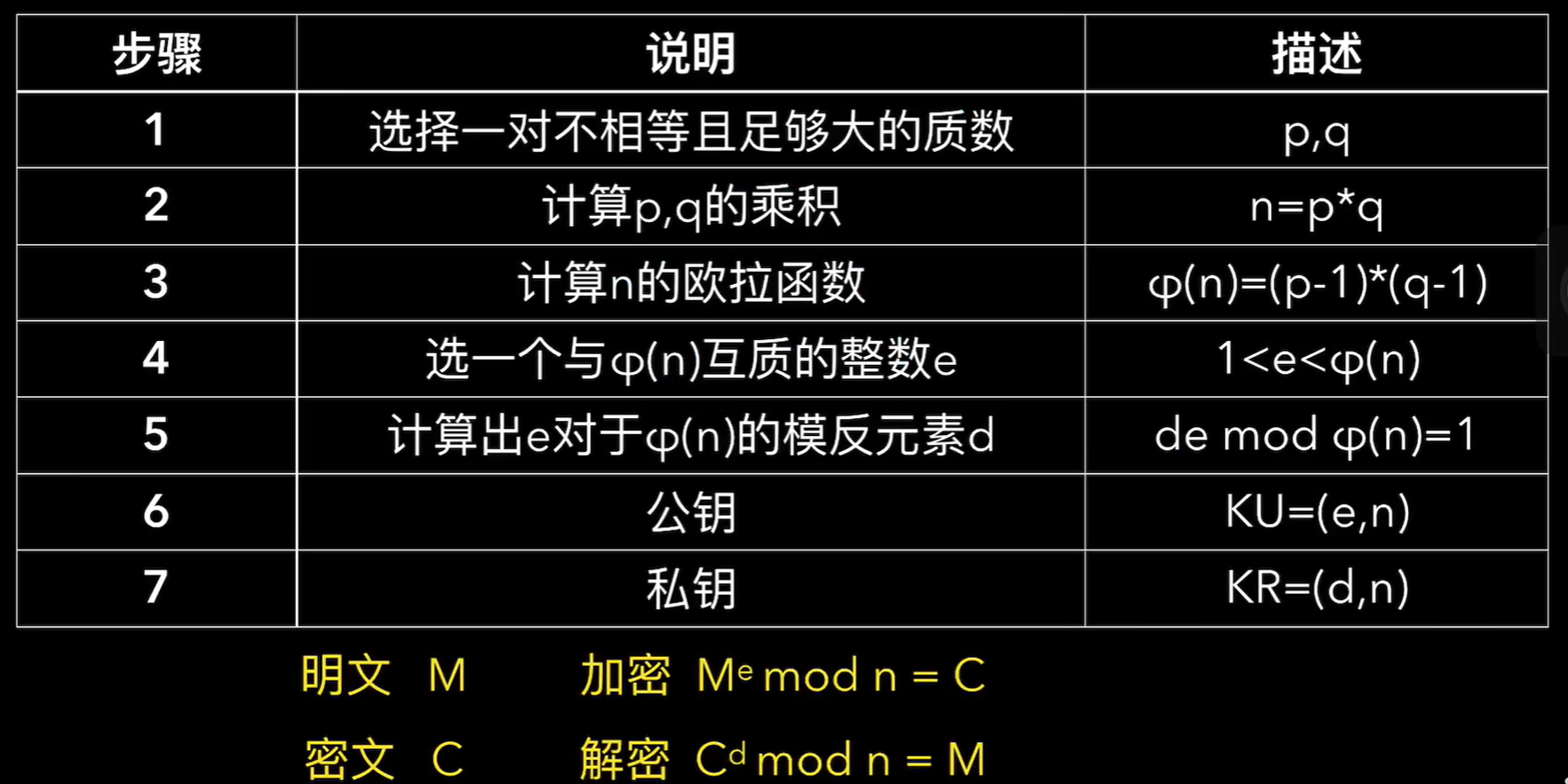
加密步骤如下图所示
1、选择一堆不相等且足够大的质数 p 和 q
2、计算 p 和 q 的乘积 n = p * q
3、计算 n 的欧拉函数 ϕ(n)=(p-1)*(q-1)
欧拉函数 ϕ(n):统计 小于n 的所有和 n 互指的数的个数。
注意:这里说的互质的数包括1
例如:ϕ(6)=2,小于 6 的数有 [1,2,3,4,5] ,和 6 有公因数的数有 [2,3,4],和 6 互质的数有 [1,5] ,所以 ϕ(6)=2
质数的欧拉函数为质数本身减一
例如:ϕ(7)=6,小于 7 的数有 [1,2,3,4,5,6] ,这些数都和 7 互质,所以 ϕ(7)=6
因为 p 和 q 均为质数,所以 ϕ(n)= ϕ(p) ϕ(q) = (p-1) (q-1)
4、选一个与 ϕ(n) 互质的整数 e ( 1 < e < ϕ(n) ,e通常取 65537 )
5、计算出 e 对于 ϕ(n) 的模反元素 d ( d*e mod ϕ(n) = 1 )
模反元素的计算需要通过扩展欧几里得算法实现,最后算出的 d 为 e 的系数
# 通过python函数实现扩展欧几里得算法,结果返回为(最大公因数,x,y) , a*x + b*y = gcd(a,b) , gcd(a,b)为a和b的最大公因数
def extended_gcd1(a,b): # 扩展欧几里得算法,通过循环实现
old_s=t=1
old_t=s=0
old_r=a
r=b
while r!=0:
q=old_r//r
old_s,s=s,old_s-s*q
old_t,t=t,old_t-t*q
old_r,r=r,old_r%r
return (old_r,old_s,old_t)6、加解密
明文为 m
密文为 c
加密算法 ( e , n )
加密算法需要知道 e 和 n
计算方法: me mod n = c
m的e次方 模n 得到密文c
# python 代码表示为 c = m ** e % n
解密算法 ( d , n )
解密算法需要知道 d 和 n,要求出 d 就需要知道 p 和 q,通过欧拉函数计算出 ϕ(n)=(p-1)*(q-1) ,再通过扩展欧几里得算法求出 e 的系数 d
计算方法: cd mod n = m
c的d次方 模n 得到明文m
# python 代码表示为 m = c ** d % n
以上就是RSA加解密的过程及其原理
加密:已知 m=3194 , 选 p=976643 , q=565583 , e=65537,求密文 c
解:先根据已知条件p,q求出 n ,再通过明文模 n 最后得到密文 c
n = p * q = 976643 * 565583 = 552372677869
c = m ** e % n = 3194 ** 65537 % 552372677869 = 348234702383
解密:已知 c=348234702383 ,p=976643 , q=565583 ,e=65537,求明文m
解:现根据已知条件 p 和 q 求出 n 和 ϕ(n) ,再通过 e 和 ϕ(n) 求出 d,最后通过 d 和 n 求出明文 m
n = p * q = 976643 * 565583 = 552372677869
ϕ(n)=(p-1)(q-1) = 976642 565582 = 552371135644
通过扩展欧几里得算法求出 e 的系数 d = 211173212133
m = c d % n = 348234702383 211173212133 % 552372677869 = 3194
以上两个例子就是加密和解密的过程了。




厉害